Risk reduction hardware-in-the-loop experiments for spacecraft Guidance, Navigation, and Control (GNC) functions using a small-scale 3DOF of experimental attitude platform. This enables the work to develop and test state-of-art control algorithms for ADCS of small satellites type missions. Our work includes the following projects:
-
Novel attitude estimation and control laws of various cases fault detection cases and investigate efficient resolutions.
-
Learning-based (e.g. Reinforcement learning) algorithms for adaptive and robust GNC.
-
Multiples of these platforms are used to demonstrate

Computational Astrodynamics
Novel n-dimensional orthogonal approximation ideas have been developed and demonstrated. Two challenging astrodynamics applications are considered:
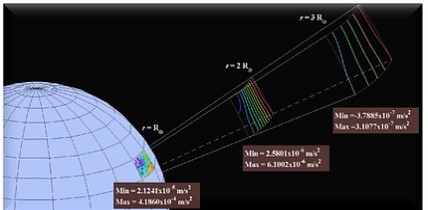
Local approximation of high degree and order geopotential models, where the global spherical harmonic series is replaced by a family of locally precise orthogonal polynomial approximations for efficient computation. Further significant improvements in computational performance are achieved by making the approximation degree radially, compatible with the truth that the highest degree approximations. Several orders of performance improvement are realized by recognizing that lower degree approximations are required as radius increases. Combining all of these strategies yielded orders of magnitude speedup for serial calculations
Orbit propagation and solution of associated boundary value problems using Chebyshev-Picard path approximation method, which is well-known to be powerful for solving these problems with over an order of magnitude speedup relative to known methods.
Further speedups have been achieved by exploiting its fundamental parallel-structure using CUDA implementation. Maximum computational performance is achieved by combining the orthogonal Finite Element Model (FEM) gravity approximations and the Chebyshev-Picard path approximation; thereby enabling truly revolutionary speedups in orbit propagation without accuracy loss.
OCEA & Algorithms Development
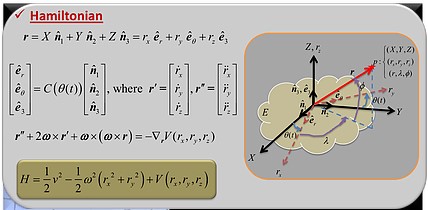
An automatic differentiation tool, Object Oriented Coordinate Embedding Algorithm (OCEA), that enables tensor-based high-order calculations for automating the generation of high-order partial derivative models. The availability of these high order partial derivative models has created a unique opportunity to investigate fundamental generalizations of many classical numerical analysis strategies and tools. Motivated by the availability of automatically generated partial derivative models, we have investigated the impact of generalizing classical iteration algorithms to incorporate higher-order sensitivity information. Examples of this work include:
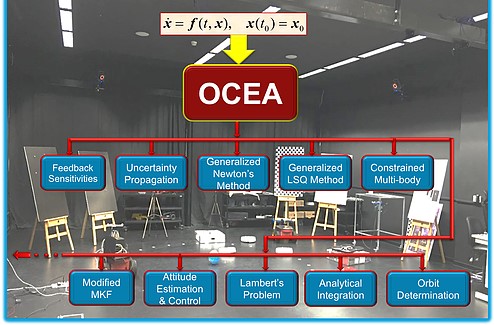
- Least Squares Differential Correction and Newton’s method.
- Lambert’s Problem
- Orbit Determination
- Attitude Determination
- Numerical Integration Methods: Applied to the problem of numerical integration of complex trajectory problems.
- Model Uncertainty Propagation
- Uncertainty Propagation
- High-order state transition tensors of the high-fidelity dynamics
- Adaptive Control
- Constrained Multi-body dynamics
- Dynamic Modeling
Implementing efficient GNC algorithms for optimal flight. Our work includes but not limited to:
- Fast Region-based Convolutional Network method (Fast R-CNN) for autonomous aerial refueling. This method adopts fast R-CNN for an onboard relative navigation solution.
- Swarm UAVs
- Objects avoidance
- tracking motion
- GNC-based cooperation of swarm agents



